★新サイト完成しました!
3秒後に自動的に移動します
変わらない方は こちらからどうぞ
http://logics-of-blue.com/%E3%83%AD%E3%83%BC%E3%82%AB%E3%83%AB%E3%83%AC%E3%83%99%E3%83%AB%E3%83%A2%E3%83%87%E3%83%AB/
前のページではNileデータを使ってローカルレベルモデルを推定 しました。とはいえ、ローカルレベルモデルとはいったい何なのかということを全く説明 していなかったので、状態空間モデル(今回はその中の一部である動的線形モデル)の一番の基礎となるこのローカルレベルモデルについて解説します。
状態空間モデル関連のページ
状態空間モデル 状態空間モデルのことはじめ
dlmの使い方
Rで正規線形状態空間モデルを当てはめる
ロー
カルレベルモデル dlmパッケージを使ってローカルレベルモデルを当てはめる
季節とトレンド dlmパッケージを使って季節成分とトレンドの入ったモデルを作る
作成日 2012年 8月 8日
最終更新 2012年 8月 8日
ローカル・レベル・モデルは、ランダムウォーク・プラス ・ノイズ・モデルともいわれます。ランダムウォークがわからないとこのモデルもわからないので、まずはランダムウォークから説明します。
ランダムウォーク
別名ドランカーズウォーク、酔歩。状態空間モデルに限らず、時系列解析ではよく出てくる言葉です。
正確な定義はともかくとして、雰囲気を書きます。
普通の乱数は、たとえば
2000年にサイコロをふって3の目が出た
2001年にサイコロを振って2の目が出た
2002年にサイコロをふって1の目が出た
2003年にサイコロを振って−2の目が出た (マイナスの目がある
サイコロだということにしてください)
2004年にサイコロをふって6の目が出た
2005年にサイコロを振って−4の目が出た
ということならば、
3,2,1、−2,6、−4 という時系列データが得られます。サイコロの目そのものですね。
つぎはこの系列がランダムウォークだったとします。すると、
2000年 3
2001年 3+2 = 5
2002年 5+1 = 6
2003年 6+(−2) = 4
2004年 4+6 =10
2005年 10+(−4)= 6
となります。
普通の乱数だと、サイコロの目ですから(マイナスがあるという変則ルールではあるけれども)、
−6〜6までの範囲しか決してとりません。
けれども、ランダムウォークだと、「一期前の値からスタートして乱数を振る」という感じのことをしているので、目の出方によっては値が10とかを超えるこ
ともあります。
ここで示したランダムウォークは、単に乱数を足していっただけのものですが、なんだか意味ありげな複雑な挙動を示します。
というのも、「たまたま」さいころが正の目ばかり出たら、このランダムウォーク系列は右肩上がりで増加していきますし、「たまたま」負の目ばかり出た
ら、逆に減少トレンドがあるように見えます。けれどもその中身は単なる乱数の累積和だったりするんですね。
ランダムウォークを使えばかなり柔軟にデータを表すことができます。
たとえば、ランダムウォークを使うと、データが緩やかに変動してく様子をうまく表すことができます。
というのも、「前期の値からスタートして乱数を振る」という作業の繰り返しなので、前期の値に近い値が来期でも出てくる可能性が高いからです。
変動は緩やかですが、ずっとサイコロで正の目が出続けると、この系列は際限なく増加していくように、上限・下限はありません。
来期の値は前期の値に似てるというのを表すのに、ランダムウォークは便利なんですね。
これでようやく、本題のローカルレベルモデルの説明に移れます。
こいつが何なのかというと、見えない状態の部分がランダムウォークしているとみなしているモデルのことです。状態がランダムウォークしていて、そ
れに観測誤差であるところのノイズが加わって生じたのが観測値だ、とみなしています。だから別名がランダムウォーク プラス ノイズモデルなんですね。
前のページの計算例では二つの分散を最尤法を使って推定しま
した。一つは観測誤差の大きさ。もう一つは状態そのものが変動するその大きさです。
正規分布だの分散だの言ってもわかりにくいかもしれないので、またサイコロの例を挙げます。
分散はさいころの例において、さいころの目がとりうる範囲だと思ってください。さいころだと −6〜6
の範囲しかとりませんでした。だから、一期前より、±6より大きく変動することはないと仮定していたわけです。これが、±10まで変動するのか、±1しか
変動しないのかを最尤法使って調べたということです。 また、このサイコロには正負
に偏りがなく、サイコロをたくさん投げたときの平均値は0になります。※
もう一度、単なるノイズとランダムウォークの違いを明確にするために、例を挙げて説明します。
最尤法をした結果、観測誤差は±7の範囲を持つことがわかり、状態の変動の大きさは±4であることが推定できたとします。
2000年の状態は10でした。
2001年は、10から±4の範囲内で動く可能性があります。 サイコロを振ったら+3になったとします。すると、2001年の状態は13です。
ノイズの大きさは常に±7なので、2001年の観測値は、6〜20の範囲内に収まるだろうと考えられます。
つぎは2002年です。2001年の状態が13で、状態は±4の範囲内で動きます。さいころを投げたら+1が出ました。よって2002年の状態は14で
す。
ノイズが加わった観測値は、7〜21の範囲内になるだろうと推測できます。
・・・・・・とこういう流れです。
サイコロを投げて状態が決まると書きましたが、そのサイコロはランダムに値を出します。じゃあ、一期先の状態はどう予測するのが正解かというと、 それは前期の値と全く同じ値を予測値として出すことです。サイコロの目が正になるのか負になるのかわからず、その平均値は0になるっていうんだっ たら、前期の値に0を足すのが最適な予測になるのは当然でしょう。ようするに、このローカルレベルモデルだけでは、将来予測には何の役にも立ちません。
よって、先ほどの例を正しく書き直すと次のようになります。
2000年の状態は10でした。
2001年は、10から±4の範囲内で動く可能性があります。 でも、サイコロの目がどんな値になるのか全くわかりません。よって2001年の状態は、
前年と同じ10と予測されました
ノイズの大きさは常に±7なので、2001年の観測値は、3〜17の範囲内に収まるだろうと考えられます・・・・・・。
もちろんカルマンフィルターを使ってモデルを推定している以上、観測データの値を加味して状態を補正しています。
たとえば、2001年の状態は10と予測されていました。その後観測値が得られて、その値が19だったとします。これは、2001年の状態を過小評価し
ていた可能性大です。そこで予測されていた状態10を補正して13だという結果となりました。
ノイズの大きさは常に±7なので、2001年の観測値は、6〜20の範囲内に収まるだろうと考えられます・・・・・・。というのを何回も繰り返し。
将来予測には役に立ちませんが、データさえ得られれば、その時の状態を推定することができるわけです。
もちろん、スムージングをすると、もっと将来の観測値も使って状態を補正することができます。
ローカルレベルモデルそのものは予測に役立ちませんが、これを発展させる感じでモデルを複雑にしていけば、少しはまともな予測を出すことができま
す
※
動的線形モデルでは、観測誤差も、状態の変動も、正規分布に従うと仮定されています。正規分布って
のは、2.24とか小数点以下の値も平気でとりますし、サイコロみたいに「絶対4より大きな数は出ない」なんて制約もありません。ここはちょっと気を付け
てください。念のため。
次は、状態空間モデルの難所というか、パッと見よくわかんない「左端」について説明します。もちろん左端というのは私の造語ですが。ほかの言い方
が難しい、文字通り「ひだりはし」の問題です。
今までの例ではさりげなく、「2000年の状態は10でした」から話を進めていましたが、この2000年の状態って、どう扱えばよいのでしょう か。グラフにすると一番左端の部分なので、私は勝手に左端と呼んでます。ほかの人に説明するときに左端って言っても通じないので気を付けてください。。
この左端の値、dlmパッケージではデフォルトで0となっています。Nileデータだと千いくつとかいう単位だったんですが、それでも、左端は 0、と指定しています。この左端の値は前のページの計算例でモデルの 「型」を表示させたときに実は出てきていて、もう一度表示すると、
> mod.Nile
$FF
[,1]
[1,] 1
$V
[,1]
[1,] 15099.75
$GG
[,1]
[1,] 1
$W
[,1]
[1,] 1468.459
$m0
[1] 0
$C0
[,1]
[1,] 1e+07
この、太字で示したm0のところです。0になってますよね。
前回、推定された状態をグラフに表示させるとき dropFirst という関数を使って、左端の値を取り除いてからプロットしていました。この理由
は、左端が0だからです。推定していないんだから、表示させると、うっとうしいことになるので、切ったんですね。ちなみに最後のC0は、左端における分散
の値です。これも勝手な値が仮定されています。
前ページの例を見ればわかるように、べつに、このままでもモデルは推定できます。なぜかというと、カルマンフィルターでは観測データを使った補正
が行われているからですね。
Nileデータは1971年から存在します。1971年の状態を推定するためには左端として1970年の状態の値が必要です。それを0だと仮定した。
で、1971年の状態は、前期の状態の値と全く同じだとみなされるので0だと予測される。1971年の実際の流量は1120でしたので、0というのは猛烈
な過小評価だ、ということですごい勢いで補正されたんですね。
前回の例だとNileFilt$mをすれば、推定された状態が表示できると書きましたが、この値は1970年からのスタートとなっています。Nile
データは1971年からスタートなのに謎に1970年が存在して、そこに0が入っているというのは、これが原因です。これをdropFirst使って排除
したと。
で、補正された状態を使って1872年以降が推定されているから、一応問題ないということです。dlmのマニュアル見てると、結構左端は0のまま推定し
ているときが多いような気がします。
左端に関してはほかにもいくつか対策があります。
一つは、左端を、データもろとも切って捨てること。Nileのデータは1872年からしかないとみなすんですね。で、新しく先端のデータとなった
1872年にお
ける左端に、1871年の観測値を入れるんです。こうやれば(観測誤差が入っているので1871年の状態そのものではないですが)ある程度正しそうな左端
を仮定してモデルを組むことができます。ただし、このやり方だと、使えるデータが一期分少なくなってしまいます。あんまり聞いたことないやり方ですが、
(ちょっと
違う解析ですが)レフェリーにこうしたら、と勧められたことがあります。
二番目は左端というパラメタも最尤法で推定してしまう方法です。推定すべきパラメタが増えてしまい、やや大変
という欠点はありますが、手持ちのデータを全部使ってモデルを組めます。
三番目は、偉い先生が決めたとか理論的な考察に基づいてなぜかもうすでにわかってるとかいう場合です。これは、わかってる値をそのまま使えばいい
です。水産の場合は神様に訊くしかないような?
実際にローカル・レベル・モデルを推定してみます。
前のページで簡単なモデルは一応推定は終わっているので、左端も一緒に推定してみます。
スクリプトはまとめてこ
ちらにおいてあります。
まずはdlmパッケージを落としてから。
> library(dlm)
としてから、計算していきます。
Step1 型の作成
build.2<-function(theta){
dlmModPoly(order=1,dV=exp(theta[1]),dW=exp(theta[2]),m0=exp(theta[3]))
}
推定すべきパラメタがいっこふえたので、,m0=exp(theta[3])が
入ってます。残りは前と一緒でdVは観測誤差の大きさ、dWは状態の変動の大きさです。
Step2 パラメタ推定
fit.2<-dlmMLE(Nile,parm=dlmMLE(Nile,parm=c(1,1,10),build.2,method="Nelder-Mead")$par,
build.2,method="BFGS")
ここで、ちょっとだけ工夫をしました。というのも、推定すべきパラメタが一個増えたので、推定がちょっと大変になっているんですね。だから、ふつうに推
定すると、変な推定値が出てしまうことがあります。
dlmMLEという関数はoptim関数という最適化関数をそのまま使っています。なので、optim関数で使える匠の技がこちらでも使えるんですね。
optim関数を使う時の工夫の方法は、文献[1]に載っています。この関数は結構推定をよくミスるので、少しでもましな推定値を出そうという先人の知恵
がたくさん載ってます。
今回は多段階最適化という技を使ってみました。まずは、dlmMLEを使って普通にパラメタを求めた後、その推定されたパラメタを初期値にしてもう一度
最適化してやる方法です。こうすれば、一番最初に適当に突っ込んだ初期値(parm=c(1,1,10)の
部分)のせいで推定結果がおかしくなるという事態を緩和することができます。
このやり方のおかげで多少ましにはなったのですが、それでも一番最初に入れる初期値によっぽど変な値を入れると意味不明な推定値が返されます。気を付け
てください。
うまく推定できているかどうかは推定結果におけるconvergenceを見るとよいです。
> fit.2
$par
[1] 9.622387 7.292300 7.013394
$value
[1] 549.63
$counts
function gradient
13 7
$convergence
[1] 0
$message
NULL
太字にした部分ですね。これが0になっていればとりあえず解がちゃんと求まったということになります。
でも、ここが0でも意味不明な推定値を返していることがあります。初期値を少し変えてみて、推定されたパラメタがどのように変化するか見ておいたほうが
いいと思います。
推定されたパラメタを使ってモデルを組みなおします
DLM.2<-build.2(fit.2$par)
> DLM.2
$FF
[,1]
[1,] 1
$V
[,1]
[1,] 15099.05
$GG
[,1]
[1,] 1
$W
[,1]
[1,] 1468.945
$m0
[1] 1111.421
$C0
[,1]
[1,] 1e+07
m0にもそれっぽい値が入りました。それっぽい値か、「絶対これはないだろ」って値かはちゃんと確認したほうがよいと思います。それくらい推定値は信用な
らないです。
あとは、前回作ったモデルと同じなので、省略します。
今度は、タイトルの通り、状態の分散を0だと仮定してモデルを組んでみます。
これはいったい何なのかというと、観測地の変動は100%観測誤差によるものであり、見えない「状態」の部分は全く変動していないということを仮定して
いるわけです。
# Step1
# モデル作成のための関数を作る
build.3<-function(theta){
dlmModPoly(order=1,dV=exp(theta[1]),dW=0,m0=exp(theta[2]))
}
# Step2
# MLEでパラメタ推定。
fit.3<-dlmMLE(Nile,parm=dlmMLE(Nile,parm=c(1,7),build.3,method="Nelder-Mead")$par,build.3,method="BFGS")
# 推定されたパラメタを使ってモデルを作り直す
DLM.3<-build.3(fit.3$par)
# Step3
# カルマンフィルター
Nile.Filt.3<-dlmFilter(Nile,DLM.3)
# Step4
# スムージング
Nile.Smooth.3<-dlmSmooth(Nile.Filt.3)
# plot
plot(Nile,col=8,type="o",main="スムージングの結果")
lines(Nile.Smooth.3$s,col=4)
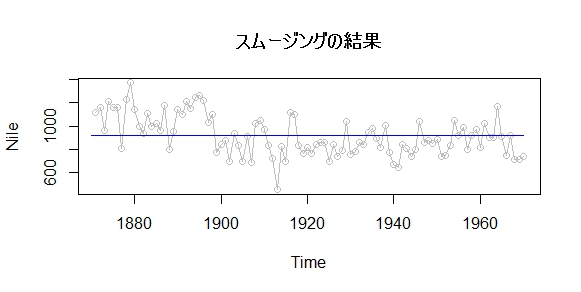
今回はスムージングの結果だけを載せていますが、まっすぐになっているのがわかると思います。
状態が全く動かないというのは、実は、ふつうの線形回帰を行った結果と一致します。
lm.model<-lm(Nile~1)
↑は、説明変数の入っていない線形回帰です。傾きが0の直線を引っ張る処理ですね。切片だけを推定したわけです。
これの切片の推定結果は
> lm.model$coef
(Intercept)
919.35
一方、dlm使って引っ張られた線はこんな値になってます。
> Nile.Smooth.3$s
Time Series:
Start = 1870
End = 1970
Frequency = 1
[1] 919.35 919.35 919.35
919.35 919.35 919.35 919.35 919.35 919.35 919.35
[11] 919.35 919.35 919.35
919.35 919.35 919.35 919.35 919.35 919.35 919.35
[21] 919.35 919.35 919.35
919.35 919.35 919.35 919.35 919.35 919.35 919.35
[31] 919.35 919.35 919.35
919.35 919.35 919.35 919.35 919.35 919.35 919.35
[41] 919.35 919.35 919.35
919.35 919.35 919.35 919.35 919.35 919.35 919.35
[51] 919.35 919.35 919.35
919.35 919.35 919.35 919.35 919.35 919.35 919.35
[61] 919.35 919.35 919.35
919.35 919.35 919.35 919.35 919.35 919.35 919.35
[71] 919.35 919.35 919.35
919.35 919.35 919.35 919.35 919.35 919.35 919.35
[81] 919.35 919.35 919.35
919.35 919.35 919.35 919.35 919.35 919.35 919.35
[91] 919.35 919.35 919.35
919.35 919.35 919.35 919.35 919.35 919.35 919.35
[101] 919.35
両方とも919.35になっていますね。ちなみに
> mean(Nile)
[1] 919.35
Nileの平均値は919.35ですから、これは単に平均値を求めたのと同じことになっているということです。
これをすれば、状態空間モデルと回帰分析の関係が多少はわかるかなと思います。回帰分析は、状態の分散が0であると仮定された状態空間モデルとみな
せるんですね。だから、状態空間モデルのほうがパワーアップしているということです。
バグや誤り等ございましたら、掲示板などにご一報ください。
参考文献
[1] 汎用最適化関数optim()の使用法
http://www.okada.jp.org/RWiki/?%B4%D8%BF%F4%A4%CE%BA%C7%C2%E7%A1%A6%BA%C7%BE%AE%B2%BD
[2] J.J.Fコマンダー、S.Jクープマン 和合肇 訳: 状態空間時系列分析入門,2008
[3] G,Petris, S Petrone, P Campagnoli: Dynamic Linear Models with R, 2009
前のページ ⇒ dlmの使い方 へ
次のページ ⇒ 季節とトレンド へ