★新サイト完成しました!
3秒後に自動的に移動します
変わらない方は こちらからどうぞ
http://logics-of-blue.com/var%E3%83%A2%E3%83%87%E3%83%AB/
Rを用いたVARモデ ル の簡単な解説と計算方法を載せます。
前回紹介したのは1変量のARIMAモデルというものでした。
これは「過去の自分のデータから将来の自分を予測する」というものです。たとえば、2000年にサンマがたくさんいたら過去の2001年にもたくさんい
ることになるだろうという風に、サンマの予報をするなら、サンマの漁獲量だけに注目してして予測をします。
でも、去年餌になるプランクトンが多かったから今年はサンマが増えた、という風に、「ほかのやつら」の影響を受けているかもしれませ
ん。
そんな場合をモデルで表して予測をしてやろうというのが今回扱うVARモデルというものになります。
VARとは Vector Auto Regressive ⇒ベクトル自己回帰モデルの略です。まえに
やったARモデルを多変量に拡張したものになります。
AR
モデルとは、たとえばサンマの来遊量を予測しようとしたとき、前年のサンマ来遊量を横軸に、翌年のサンマ来遊量を縦軸においてプロットして回帰分析をやっ
たのと大体同じものでした。これを多変量に応用します(名前の通り、MAモデルはVARにおいては加味されません。VARMAモデルはあまり使われない
し、省略します)。
具体的にはこんな感じ
VARモデル
今年のサンマ = 去年のサンマ×傾きA + 去年のプランクトン×傾きB +切片C
今年のプランクトン= 去年のプランクトン×傾きD + 去年のサンマ×傾きE +切片F
傾きとか切片っていうのは、回帰分析をイメージして書いてみました。φとか使うとややこしく見えますもんね。「傾きA」とか書いているのは、各々の傾きは
別の値だよ(傾きAと傾きBは異なる)ということを見えやすくするために入れただけです。こういうパラメタはちゃんと全部別々に推定されます。
ここで、もしもサンマを一変量のARモデルで表したならば、こうなります。
ARモデル
今年のサンマ = 去年のサンマ×傾きG + 切片H
これにプランクトンの値が加味されただけ。簡単なんですけど、ほかのやつらの影響を組み込んだ方がうまく予測できそうな気がしますよ
ね。
経済学とかだと、変数の間の関連性を調べる(サンマとプランクトンの関係とか)ためにさらにいろいろな解析が行われるみたいですが、今回は省略。予測だ
けをやります。
今回使ったRのスクリプトはここから見れます。
今回使うのは vars というパッケージです。
これをRの左上にある「パッケージ」→「パッケージのインストール」をやってインストールしてから
library(vars)
をやれば準備完了。これを使えば例によってAICを使って簡単にモデルを構築できます。モデル選択についてはこちらをみてく
ださい。
このモデルの場合は、「何期前までを使って予測するか?」(モデルの次数とか言ったりします)をAICを使って選ぶということになります。どの変数を使っ
て予測すればよいかということは分かりません。予測に聞く変数かどうかはGrangerの因果検定をやれば調べられますが、今回は省略します。
今回は、このパッケージに入っているCanadaを使います。なんかよくわかりませんが経済データだそうです。マニュアルの例でも紹 介されていたデータなのでそのまま使いました。四つの変数が入ってます。
data(Canada)
>
Canada
e
prod
rw U
1980 Q1 929.6105
405.3665 386.1361 7.53
1980 Q2 929.8040
404.6398 388.1358 7.70
1980 Q3 930.3184
403.8149 390.5401 7.47
1980 Q4 931.4277
404.2158 393.9638 7.27
1981 Q1 932.6620
405.0467 396.7647 7.37
・・・・略
Canadaの1999以降は切って、テスト用に残しておきます。まえは別のやり方でやってましたが、window()関数を使えば簡単に切れます。
Canada.1998<-window(Canada,end=c(1998,4))
で、VARモデルを推定する関数は文字通りVAR
()というやつです。次数の決定はVARselect
()でOK。データはトレンド付かトレンド無かを選ぶことができます。
トレンドなし、定数付(切片が0でない)で最適な次数を調べます。
>
VARselect(Canada.1998, lag.max = 5, type="const")# constで定数
$selection
AIC(n)
HQ(n) SC(n) FPE(n)
3
2
1 3
$criteria
1
2
3
4
5
AIC(n) -5.968164387
-6.316081011 -6.385300206 -6.112389835 -5.87693104
HQ(n)
-5.714700702 -5.859846377 -5.726294624 -5.250613305 -4.81238356
SC(n)
-5.330789774 -5.168806707 -4.728126212 -3.945316150 -3.19995766
FPE(n)
0.002561326 0.001816949 0.001714569
0.002300861 0.00301527
AIC基準では次数3が最もよさそうということになりました。この結果を用いてVARモデルを推定します
lag1<-VARselect(Canada.1998,
lag.max = 5, type="const")$selection[1]
var.1<-VAR(Canada.1998,p=lag1,type="const")
計算結果は長いので略。 var.1 と打ち込めばモデルの傾き(係数)とかいろいろ出てきます。
予測します。
yosoku<-predict(var.1,
n.ahead = 8, ci = 0.95, dumvar = NULL)
kekka<-ts(yosoku$fcst$e[,1],start=1999,frequency=4)
sita<-ts(yosoku$fcst$e[,2],start=1999,frequency=4)
ue<-ts(yosoku$fcst$e[,3],start=1999,frequency=4)
これで、Canadaデータのうちeという変数に関する予測とその95%区間が求まります。
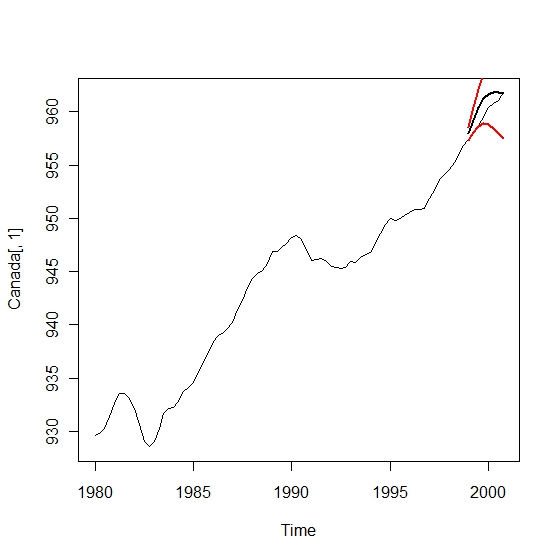
まぁまぁいけてそうです。
遠い先まで予測してみると(実用性はたぶんありません。予測結果の特徴を見るためのものです)
yosoku<-predict(var.1,
n.ahead = 100, ci = 0.95, dumvar = NULL)
kekka<-ts(yosoku$fcst$e[,1],start=1999,frequency=4)
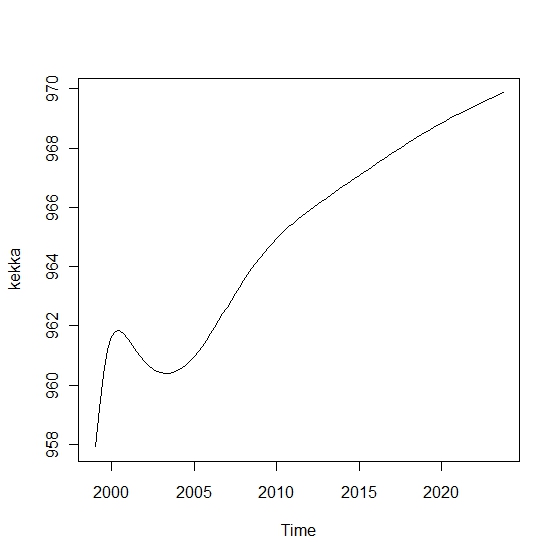
長期予測のやり方としては、サンマとプランクトンの例で行くと、
1 過去のサンマとプランクトンからサンマを予測
2 同様にプランクトンも予測
3 予測されたサンマ・プランクトンからサンマを予測
4 同様にプランクトンを・・・・・・という手順です。
まぁRが勝手にやってくれるんで知らなくていいかもしれませんが。でも、長期予報はあんまりあてにならない(予測結果を使って予測する わけだから)というのは直感的にわかるでしょう。
同様にトレンド付のモデルも推定できます。
lag2<-VARselect(Canada.1998,
lag.max = 5, type="both")$selection[1]
var.2<-VAR(Canada.1998,p=lag2,type="both")
結果は省略。bothっていうのは、切片と傾き両方入ったモデルだと考えてください。
ちなみに、普通の教科書では傾きは係数、切片は定数項という名前で書かれていることが多いと思います。
実はVARモデルは前に書いたARMAモデルで記述することができます。数式の上ではそうなんですが、実感わかないですね。ここら辺は山本 拓 の参考文 献がわかりやすいです(関係ないけれども、ARモデルとMAモデルの変換などもこの文献がわかりやすかった。実例があるので)。でも、ARMAだとかなり 長い次数が必要なのがVARだととても少なくて済むようです。
多変量ARだからMultiple AR でMARかとおもいきやVARという名称。ここら辺は数式見ないと実感できないかもしれません。B(モデル名)でベクトル表示して係数を見ることができま す。なれたらこっちの方が見やすいかもしれません。
扱う変数の数が増えると(たとえばサンマとプランクトンだけではなくイワシとアジとサメと海鳥も追加とか)推定すべきパラメータ(傾 き)がものすごい量になってしまうのであまり実用性がなくなってしまうので注意。
VAR
のパワーアップバージョンでSVARとかがあります。これはVARモデルだと「過去が今に影響を与えている」ということしかモデルで表せられなかったの
が、SVARだと「同じタイミングでもサンマとプランクトンは影響し合っている」ということを明示的にモデリングできます。同じくパッケージvarsで計
算できます。これ以外にもたくさん発展形があります。
あと、ベイズつかってパラメタ推定もできます。パッケージMSBVARで計算できます。
参考文献
沖本竜義:計量時系列分析、朝倉書店、東京、2010
RjpWiki アーカイブス 時系列オブジェクト一覧
http://www.okada.jp.org/RWiki/?RjpWiki%20%A5%A2%A1%BC%A5%AB%A5%A4%A5%D6%A5%B9
山 本 拓:時系列分析とその経済分析への応用、大蔵省財政金融研究所「フィナンシャル・レビュー」
松本 惇: 統計ソフトRによるVAR入門
varsマニュアル: http://cran.r-project.org/web/packages/vars/vars.pdf
前のページ ⇒ 時
系列解
析 実践編 へ