Home＞Ｒな予測＞時系列解析　実践編

時系列解析　実践編

★新サイト完成しました!
３秒後に自動的に移動します

変わらない方は こちらからどうぞ
http://logics-of-blue.com/%E6%99%82%E7%B3%BB%E5%88%97%E5%88%86%E6%9E%90_%E5%AE%9F%E8%B7%B5%E7%B7%A8/

Rを用いた時系列解析 の実践例を載せます。

使用データ

　シミュレーションデータと、Rにもともと入っているサンプルデータを用います。

シミュレーションデータはこちら

set.seed(1)
d<-arima.sim(n=200,model=list(order=c(2,0,2),ar=c(0.2,0.7),ma=c(0.7,0.3)),sd=sqrt(1))

ARIMA(２,０,２）モデルが推定できれば正解です。こちらはARMA過程であって、和分過程ではありません。「定常過程」とも言 われる安定した挙動を示します。
　「定常過程」についての詳しい説明は参考文献をどうぞ。

もう一つ、和分過程のデータも用意してみます。

dd<-arima.sim(n=200,model=list(order=c(2,1,2),ar=c(0.2,0.2),ma=c(0.7,0.3)),sd=sqrt(1))

さっきの和分過程で無いデータとは大分と違った挙動をすることを確かめます。

　そして、季節的周期変動があるデータとして、AIｒPassengerというデータを用います。これは、月別国際空港路線総顧客数 （単位　千人）のデータで、時系列解析のサンプルデータとして割と有名なものです。

data<-ts(AirPassengers[1:132],start=c(1949,1),frequency=12)

　AirPassengersのうち、最後の一年間はテスト用として省いておきました。最後の一年間をモデルを使って予測してみて、正 しいかどうかを見極めます。
　ts(）で時系列データとして読み込むと 言う指示を。AirPassengers[1:132]でAirPassengesr というデータにおける１〜１３２番目のデータのみを用いると言う指示を。start=c(1949,1)で1949 年の単位1からスタートということを。frequency=12で 一単位は一年間の12分の一⇒要するに月単位データだと言うことを表します。だから、startは1949年の1月ということになります。

モデリングと予測　１、和分過程で無いデータ

　まずはモデリングしてみます。パッケージforecastをインスと−ルしてから……

library(forecast)
model<-auto.arima(d,ic="aic",trace=T,stepwise=F,start.p=0, start.q=0, start.P=0, start.Q=0)

> model
Series: x
ARIMA(2,0,2) with zero mean    

Coefficients:
         ar1     ar2     ma1     ma2
      0.2784  0.6334  0.5165  0.2595
s.e.  0.1007  0.0988  0.1126  0.0781

sigma^2 estimated as 1.003:  log likelihood = -285.46
AIC = 580.93   AICc = 581.24   BIC = 597.42

　うまいこと、ARIMA(2,0,2)モデルを選択できました。ちなみに、たまに（というか、よく）本来のモデルとは別のモデルを 「もっとも良い」として引っ張ってきてしまいます。それだけ時系列モデルを正確に選ぶのは難しいということでしょうか？

　モデルが「良い」モデルかどうかは、残差（予測値−実測値）がきれいにばらついているかどうかを確かめることによって、ある程度判断 できます。
　要するに、予測値の方が実測値よりも常に大きいとかいうような系統的な誤差があれば失敗ということになります。また、残差に自己相関があれば、これはこ れでうまくモデリングできていないことになります。誤差はあくまでも、誤差らしくあるような状態が理想である訳。

tsdiag(model)

とすれば、こ んなグラフが出てきます。
　 ３つグラフが出てきますが、一番上が残差のプロット。２番目が残差の自己相関です。これはなるべく小さい方がよいです。３番目が残差が本当に「誤差らしい 誤差（ホワイトノイズ）」になっているかの検定プロットです。丸いぽつぽつが上の方にあって、青い線を下回らないようであれば、ホワイトノイズと見なすこ とができます。

最後に予測をしてみます。

> forecast(model, level = c(50,95), h = 50)
    Point Forecast       Lo 50    Hi 50      Lo 95    Hi 95
201      6.3921558  5.71668873 7.067623  4.4293520 8.354960
202      5.8279690  4.96511994 6.690818  3.3206617 8.335276
203      5.6711917  4.52626393 6.816119  2.3442069 8.998176
204      5.2701904  4.00019735 6.540183  1.5797850 8.960596
205      5.0592572  3.64173900 6.476775  0.9401662 9.178348
206      4.7465425  3.23548789 6.257597  0.3556491 9.137436
・・・・・・・・・・・・・・・いか略

level = c(50,95)とすると、９５％予測区間と、５０％予測区間が両方同時にもとまります。ｈ＝５０は、５０期先まで予測すると いう意味です。

プロットしてみます。今度は200期先まで

plot(forecast(model, level = c(50,95), h = 200))

モデリングと予測　２、和分過程

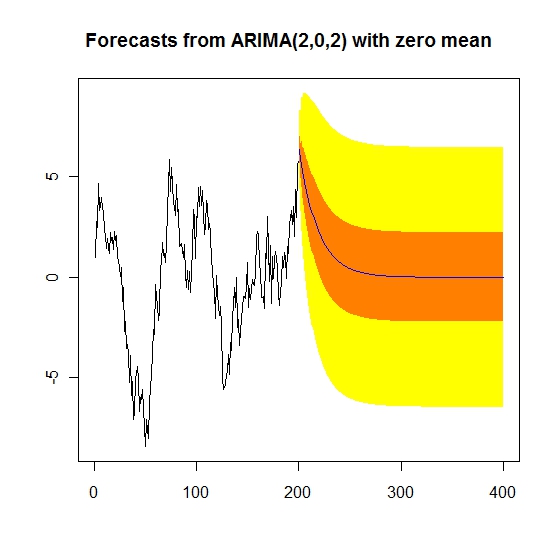
　今度は 和分過程のモデリングをしてみます。

予測区間のとられ方がかなり変わるので、そこに注目すると特徴がよくわかります。

model2<-auto.arima(dd,ic="aic",trace=T,stepwise=F)

> model2
Series: x
ARIMA(1,1,2)                   

Coefficients:
         ar1     ma1    ma2
      0.3360  0.5108  0.368
s.e.  0.1163  0.1127  0.079

sigma^2 estimated as 1.124:  log likelihood = -295.98
AIC = 599.95   AICc = 600.16   BIC = 613.15

本当はARIMA(2,1,2)のはずなんですが、ARIMA(1,1,2)モデルを採択してしまいました。ちなみに、各モデルの AICを計算してやると、

model.212<-arima(dd,order=c(2,1,2))    #ARIMA(2,1,2)モデルの推定

> AIC(model.212)
[1] 601.4864
> AIC(model2)
[1] 599.9525

と なり、やはり、本来のARIMA(2,1,2)よりも、ARIMA(1,1,2)の方がAICが小さいようです。こんなこともシミュレーションしてやれば よく起こります。シミュレーションデータでさえこうなのですから、実際のデータを予測するのはさらに大変そうだということが分かります。
　たとえば、モデルを作るのに用いるデータを、一体どれくらいの期間の長さを使えばいいのか、長すぎても短すぎても余り良くない……なんていうことを考え て行くと、かなり難儀します。今回はそういう難しい話は無視して予測してしまいました。

今回は残差プロットは無視して、先に予測をしてみます。

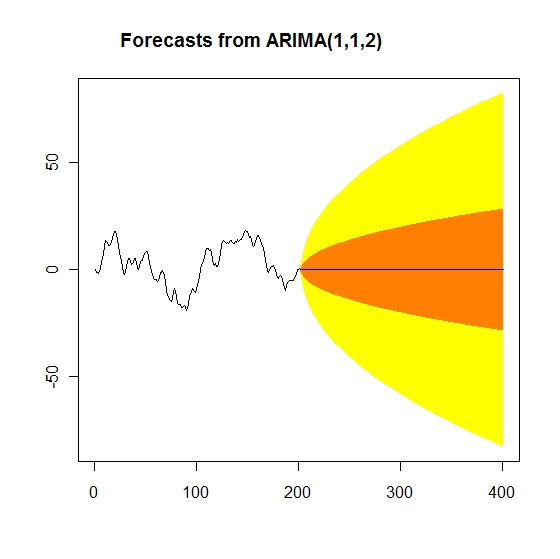
時が経つにつれて、予測幅（９５％の確率でとりうる値の幅）がどんどん大きくなっていきます。これが和分過程の特徴です。ようするに、 精確な予測が難しくなっているわけです。

　元々のデータのグラフの形も、和分過程で無いものと比べると、大分と違うことが見て取れると思います。

モデリングと予測　３季節変動データ

　最後に、季節変動データの予測です。SARIMAモデルもauto.arimaで勝手に推定してくれるので、全部任せてしまうことに します。今回は情報量基準にBICを使ってみました。

　model3<-auto.arima(data,ic="bic",trace=T,stepwise=T)　#ic= aic , aicc　でも可

> model3
Series: data
ARIMA(0,1,0)(0,0,2)[12]                   

Coefficients:
        sma1    sma2
      1.0921  0.6522
s.e.  0.1115  0.0936

sigma^2 estimated as 247.2:  log likelihood = -556.83
AIC = 1119.66   AICc = 1119.85   BIC = 1128.29

　こちらも1次の和分過程となりました。増加や減少トレンドは、和分過程としてモデリングすると上手く表すことができます。
　予測と実際の結果を合わせてプロットしてみます。

plot(forecast(model3, level = c(95), h = 12),type="o")    
#95%予測区間を12期先（＝12か月＝1年先）まで予測
lines(AirPassengers)

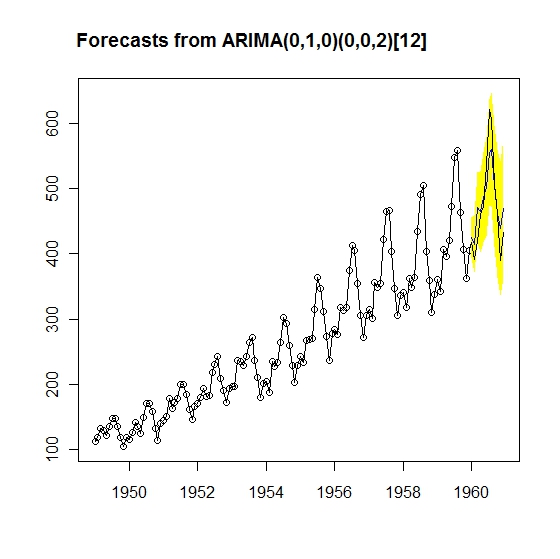
青線が予測値、黒線が実測値です。まぁまぁうまく予測できていることが分かります。

参考文献

沖本竜義：計量時系列分析、朝倉書店、東京、２０１０

田中孝文：Rによる時系列分析入門、CAP出版株式会社、東京、２００８

RjpWiki　アーカイブス　時系列オブジェクト一覧　
http://www.okada.jp.org/RWiki/?RjpWiki%20%A5%A2%A1%BC%A5%AB%A5%A4%A5%D6%A5%B9

Package ‘forecast’　説明書（PDF)
http://cran.r-project.org/web/packages/forecast/forecast.pdf

前のページ　⇒　時系列解 析　理論編　へ
次のページ　⇒　多変量時系列モデル　1VARモデル　 へ