★新サイト完成しました!
3秒後に自動的に移動します
変わらない方は こちらからどうぞ
http://logics-of-blue.com/%E5%B9%B3%E6%BB%91%E5%8C%96%E3%82%B9%E3%83%97%E3%83%A9%E3%82%A4%E3%83%B3%E3%81%A8%E5%8A%A0%E6%B3%95%E3%83%A2%E3%83%87%E3%83%AB/
Rを用いた平滑化スプライン・加法モデルの簡単な解説と計算・予測方法を載せます。
単回帰・重回帰分析との比較を交えて説明します。
作成日 2012年 5月 29日
最終更新 2012年 6月 28日
平滑化とはなんでしょうか。正確な定義ではありませんが、ものすごく簡単に言うと、「散布図にニョロニョロした線を引っ張ること」です。もう
ちょっと正確に(?)いうと、ある程度なめらかなニョロニョロした線を引っ張ることです。
以前に単回帰分析や重回帰分析に
ついて説明しました。単回帰分析は散布図に直線を一本引っ張る作業と説明したと思います。線を引くことで、たとえば気温が高くなるとビールがよく売れるな
んていう関係が明らかになったり、気温が25度の時には平均するとビールが○本売れるなんていう予測も可能になりました。なんで線を引っ張ることが予測に
つながるかというと、「線が引ける」とは「温度とビールの関係を表せている」ということを意味しているからです。温度と売り上げの関係があらわせたんだっ
たら、その関係を使えば温度から売り上げが予測できますよね。
上記のような回帰モデル(以下では線形回帰と呼びます)は非常に有用なのですが、線形の関係しか表現できないという制約があります。これは何かという
と、たとえば、気温が1度上がったらビールが10本多く売れるという関係が、どのような状態であってもずっと成り立つと考えているということです。今の気
温が10度であったとき、11度になったら10本多く売れる。今の気温が40度であっても、41度になったら10本多く売れる。こんな風に考えるんです
ね。
でもこれは結構おかしな話です。気温が40度もあったら、お客さんは暑くて外に出る気力がなくなって、むしろ売り上げは下がってしまうかもしれません。
こういうのは非線形といいます。こういう非線形な関係をモデル化するのに、今回説明する平滑化スプラインは非常に便利です。
単回帰分析をニョロニョロさせたのが平滑化スプラインだとしたら、それの重回帰バージョン(要するに説明変数(温度とか天気とか)を増やしてビールの売
り上げを予測しようとするモデル)が加法モデルです。
平滑化スプラインの仕組みについてごくごく簡単に説明します。
まず、「補間」について説明します。データは「点」として得られるもので、ふつうは「線」としては得られません。どういうことかというと、気温14度の
時のビールの売り上げという「気温と売り上げのセット」と15度の時の売り上げという「気温と売り上げのセット」は、散布図にプロットするとちょっと離れ
たところに点が打たれることになります(当然ですが)。じゃあ気温が14.236度という激しく中途半端な状態だったその瞬間にいったいどのくらいビール
が売れていたのかを帳簿につけないといけない、そんな(多分起こりえないけど)緊急事態に直面した時は補間を使えば解決できます。
補間は、ちょっとした前提を置いたうえで、点と点の間を滑らかな (これは専門用語でいうところの滑らかです。難しく言うと微分可能な)
線でつないでいきます。こうすれば、データが得られていない中途半端な状況にも対応することができます。
じゃあ将来の予測をするときは補間された結果を使えばいいのか、というとそんな簡単にはいきません。
たとえば気温が21度の時だけ偶然近くで花見が勃発してビールがめちゃくちゃ売れたとします。じゃあ気温21度の時にはすごくたくさん売れるという予測
を立てればいいかというと、ちょっと無茶でしょう。気温が21度でも桜が咲いていない年もあるかもしれません。でも、暑くもなく寒くもない適温だとお客さ
んも気分がよくなってビールの売り上げは確かにちょっとは増えるかもしれない。こんな微妙な関係(21度にこだわりすぎない。でも21度付近ではそれ以外
の気温(たとえば15度とか28度とか)よりも売り上げが高くなる)をモデリングしたい。そこで出てくるのが平滑化スプラインです。
平滑化スプライン君はこう考えます。
●条件1
散布図はなんだか21度付近を山にして売り上げが増えているように見えるなぁ。データはなるべく忠実に再現したいから予測値(散布図に引っ張る線)はなる
べくデータ点を通るように引っ張りたいな
●条件2
でもこの21度ってのはまぐれかもしれないし、22度でガクッと売り上げが下がって23度でまた復活ってちょっとグネグネしすぎだな。一貫性がないな。よ
くないな。グネグネしすぎると外れ値の影響がすっごくひびいちゃうな。あんまりグネグネしすぎないほうがいいな。
この2つの条件はトレードオフの関係にあります。トレードオフとはどちらか片方を良くすればもう片方が悪くなるということです。データ点をなるべく通るよ
うにしたいなら、当然引っ張るべき線はグネグネになるし、グネグネじゃないようにしたら(極端な話単なる直線にしたら)21度付近で売り上げが増加すると
いう貴重な知見を見失ってしまいます。
そこで、「どのくらいグネグネにするか」を決めたうえで、その「グネグネ度」に従って「ほどほどにニョロニョロ」な線を引っ張ることになります。(ちな
みにグネグネ度のことは平滑化パラメータと呼ばれます。)
では、ちょうど良いグネグネ度はどのようにして見つければよいのでしょうか。これにはクロスバリデーション(CV)や一般化クロスバリデーション
(GCV)を使います。
GCVはちょっと難しいのでCVについて説明します。CVのやり方はすごく単純です。データが{1番・2番・3番…10番}と10個手に入っていたとし
ます。そのときまずは1番目のデータを取り除いた状態でモデルを作ります。そして、作られたモデルでさっき除外していた1番目のデータを予測する。そして
その予測誤差を求める。次は2番目のデータを除外してモデルを作ってからそのモデルを使って2番目のデータを予測する。次は3番目の……と全部のデータに
対してやっていき、最終的に求められる予測誤差、これが小さいモデルが良いモデルだとみなします。
補間の悪い点として「21度の時に桜が咲いていたのは今年だけかもしれない。来年再来年の春において気温21度の時はあまりビールが売れないかもしれな
い。でもそんな状況を無視して予測してしまう」というのがありました。手持ちのデータを信頼しすぎてしまっていたんですね。そこで、データを一つずつ抜い
てテストしてやることで「未知データへの予測精度」をある程度高められるモデルを作ることができるだろうということです。
実際にRでやってみます。
やり方はいろいろあるんですが、今回はmgcvというパッケージを使います。パッケージをダウンロードした後で、
library(mgcv)
としてやれば準備OKです。今回はサンプルデータとして airquality というものを使いました。これは
head(airquality)
> head(airquality)
Ozone Solar.R Wind Temp
Month Day
1
41 190 7.4
67 5 1
2
36 118 8.0
72 5 2
3
12 149 12.6
74 5 3
4
18 313 11.5
62 5 4
5
NA NA 14.3
56 5 5
6
28 NA 14.9
66 5 6
というような環境データです。これを用いてTempでOzoneを予測するモデルを作ってみます。比較のために線形回帰での予測モデルも合わせて記
します。
lm.model<-gam(Ozone~Temp,data=airquality)
# 線形回帰
gam.model<-gam(Ozone~s(Temp),data=airquality)
# 平滑化スプライン
gam()というのは後で説明する加法モデルを推定する関数ですが、平滑化スプラインもできるので、まとめてこれでやってしまいます。
計算はとても簡単で1行で済んでしまいます。書き方も線形回帰の時とほとんど同じです。ただし説明変数(この場合Temp)にs()をつけているのが違
います。s()がついていると平滑化をしてくれます。ついていないと単なる線形回帰と同じことをします。だから上でやったgam(Ozone~Temp,data=airquality)は lm
(Ozone~Temp,data=airquality) とやっても同じ結果が得られます。
中身を取り出してみます。
summary(lm.model)
>
summary(lm.model)
Family: gaussian
Link function: identity
Formula:
Ozone ~ Temp
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)
-146.9955 18.2872 -8.038 9.37e-13 ***
Temp
2.4287 0.2331 10.418 < 2e-16 ***
---
Signif. codes: 0 ‘***’
0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
R-sq.(adj) =
0.483 Deviance explained = 48.8%
GCV score = 572.23 Scale
est. = 562.37 n = 116
summary(gam.model)
> summary(gam.model)
Family: gaussian
Link function: identity
Formula:
Ozone ~ s(Temp)
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)
42.129 2.044
20.61 <2e-16 ***
---
Signif. codes: 0 ‘***’
0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Approximate significance of
smooth terms:
edf Ref.df F p-value
s(Temp) 3.771 4.689
30.77 <2e-16 ***
---
Signif. codes: 0 ‘***’
0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
R-sq.(adj) =
0.554 Deviance explained = 56.9%
GCV score = 505.64 Scale
est. = 484.84 n = 116
線形回帰をやった時には傾きが約2.43となっていました。気温が高くなるとオゾンも高くなるようです。一方平滑化スプラインのほうは傾きが表示
されていません。当たり前ですね。ニョロニョロした線なんですから傾きなんてあるはずがありません。平滑化スプラインはノンパラメトリック回帰の一種で
す。ノンのつかない普通のパラメトリックとは、たとえば線形回帰みたいに「傾きと切片という二つのパラメタが推定できればモデルが推定できる」というやつ
らのことです。一方今回扱うノンパラメトリック回帰はそんな風に「少ないパラメタを推定するだけでモデルが求まる」というやり方を取りません。だから傾き
とかのパラメタは表示されません。いろんな人から「傾きが出ないんだけどどうしよう」と聞かれるんですが、これはこの解析の仕様です。
とはいえp値は両方表示されます。p値とは、今までに何度か出てきましたが「温度はオゾンに影響を与えているかもしれない。しかし、そのように見えるの
は単に偶然のなす所業なのだと考えることもできるはずだ。じゃあオゾンは温度に影響を受けておらず単に偶然によって今回のような結果が生じたと仮定した
ら、そんなことが起こるのはいったい何%か?」を表したものです。線形回帰でも平滑化スプラインでもp値はものすごく小さな値になっているのが見て取れま
す(<2e-16)。偶然だとみなせる確率がもの
すごく小さいんだから偶然じゃない。だから温度はオゾンに影響を与えているだろうということになります。
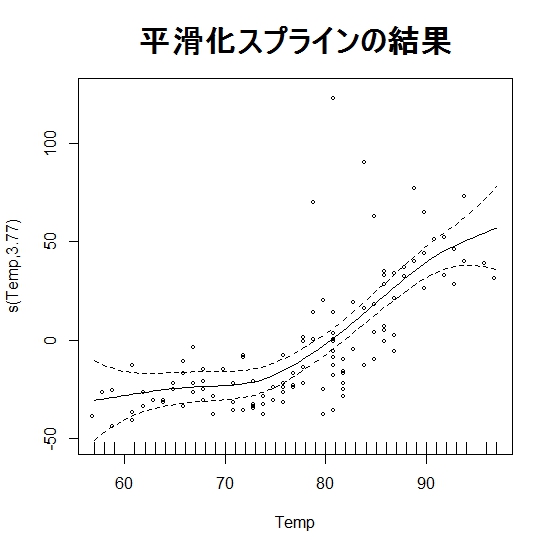
平滑化スプラインの結果は(なんせ傾きとかがわからないので)基本的には図示して示すことになります。以下の関数で簡単に描けます。
plot(gam.model,residuals=T,se=T,pch="。",
main="平滑化スプラインの結果",cex.main=2)
residuals=T,はデータの点も表示しますよという指示です。デフォ
ルトはF。se=Tは引っ張られた線の信頼区間(推定された平均値の95%区間)も
一緒に図示してねという指示。あとは点の形の指定やタイトルとタイトル文字の大きさの指定です。
線形回帰と平滑化スプラインの結果を比較する意味で、両者のやり方で線を引っ張った結果を描きます。
new<-data.frame(Temp=seq(min(airquality$Temp),max(airquality$Temp),0.1))
lm.pred<-predict(lm.model,new)
gam.pred<-predict(gam.model,new)
plot(airquality$Ozone~airquality$Temp,xlab="Temp",ylab="Ozone",
main="推定結果",cex.main=2,cex.lab=1.5)
lines(lm.pred~as.matrix(new),col=2,lwd=2)
lines(gam.pred~as.matrix(new),col=4,lwd=2)
legend("topleft",lwd=2,col=c(2,4),legend=c("線形
回帰","平滑化スプライン"))
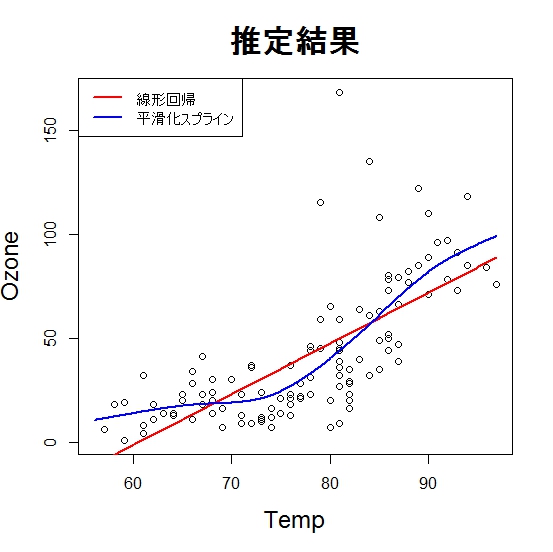
この結果を見ると、Tempが75くらいの時まではちょっとオゾンは少なめで、逆にそれ以降は急に増え始める、という関係がありそうだなというこ
とが、わかります。
非線形な予測を出すことはRを使えば簡単です。でも、本当にこんな複雑なモデルを使う必要はあるのでしょうか?
モデル選択で説明したように、「とりあえず
複雑なモデルをつくっときゃいい」というものでは決してありません。複雑なモデルのほうが逆に予測精度が下がるなんてことはざらにあります。難しい解析が
使えるということが自慢できたって誰の役にも立てません。役に立つモデルを作って、精度よく予測するためには「本当にその複雑さは必要か?」を常に考えな
ければならないでしょう。
というわけで、線形モデルを使うべきか、非線形モデルを使うべきかを判定します。判定の方法は例によってモデル選択です。今回は検定を使ったやり方を示
します。
計算は簡単。一行で終わります。
anova(lm.model,gam.model,test="F")
>
anova(lm.model,gam.model,test="F")
Analysis of Deviance Table
Model 1: Ozone ~ Temp
Model 2: Ozone ~ s(Temp)
Resid. Df Resid.
Dev Df Deviance F
Pr(>F)
1
114.00
64110
2
111.23 53929 2.771
10181 7.5783
0.0001803 ***
---
Signif. codes: 0 ‘***’
0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
p値に下線をつけておきました。今回の検定は以下のような作業です。
単純な線形回帰よりも複雑なモデルを作ってみた。すると、当てはまりの精度(引っ張られた線が予測値です。で、その予測値とデータ点との距離の小さ
さのことが当てはまりの精度です。)が向上した。でも、その当てはまりの向上は単なる誤差によるものではないのか。当てはまりの向上が単なる偶然だと仮定
したとき今回の結果が起こりうるのは何%か?
⇒結果:0.0001803
= 0.01803%
⇒すごく小さい確率
⇒偶然じゃない。やっぱりニョロニョロしてたんだ。
一行でできるプログラムって、あまりにも簡単すぎて何をやっているのか忘れてしまう方もいるかと思ったので、少々くどいですが載せておきました。
上記のように、たった一行で計算できてしまうんですが、少し時間をかけて計算してみます。
計算結果を中に詰め込んだオブジェクトである lm.model や gam.model
にはいろいろな情報が詰め込まれています。その情報を使えばそれほど苦も無く同じ計算ができるのだということを実感していただくために、計算過程を載せて
おきます。予測とは直接関係がないので、興味のない方は無理して”解読”する必要はありません。さらっと流してください。
オブジェクトの中身は names() という関数で表示できます。
names(summary(gam.model))
> names(summary(gam.model))
[1]
"p.coeff"
"se"
"p.t"
"p.pv"
[5]
"residual.df"
"m"
"chi.sq"
"s.pv"
[9]
"scale"
"r.sq"
"family"
"formula"
[13]
"n"
"dev.expl"
"edf"
"dispersion"
[17]
"pTerms.pv" "pTerms.chi.sq"
"pTerms.df" "cov.unscaled"
[21]
"cov.scaled"
"p.table" "pTerms.table"
"s.table"
[25]
"method" "sp.criterion"
中身を抽出するには オブジェクト名$中身の名前 をすればいいです。これを使って検定してみます。
DF<-summary(gam.model)$n
gam.dev<-sum(resid(gam.model)^2)
lm.dev<-sum(resid(lm.model)^2)
gam.df<-DF-summary(gam.model)$residual.df
lm.df<-DF-summary(lm.model)$residual.df
F<-((lm.dev-gam.dev)/(gam.df-lm.df)) / (gam.dev/(DF-gam.df))
F
> F
[1] 7.578315
1-pf(F,gam.df-lm.df,DF-gam.df)
>
1-pf(F,gam.df-lm.df,DF-gam.df)
[1] 0.000180271
ほかにもいろいろとやり方はあるでしょうが、その一例です。何となく雰囲気をつかんでいただければ、と思います。
実は先ほどの gam() 関数を使うと最適なグネグネ度をGCVを使って勝手に選んできてくれます。便利ですね。
でも、Rにおまかせだと何度も出てきた「グネグネ度」のイメージがしにくいかなと思うので、ちょっと丁寧に見てみます。
gam()では sp という追加のパラメタを指定してやることで手動でグネグネ度を設定できます。そこで、グネグネ度を変えたときのGCVの値 をプロットしてみます。GCVはCVと似たようなものなので、小さければ小さいほど予測精度は高い良いモデルだとみなされます。ついでに最適化されたグネ グネ度の時のspとその時のGCVも合わせてプロットしました。
sp<-seq(from=0.001,to=0.1,by=0.001)
GCV<-numeric()
for(i in 1:length(sp)){
g.m<-gam(Ozone~s(Temp),sp=sp[i],data=airquality)
GCV[i]<-g.m$gcv.ubre
}
plot(GCV~sp,main="GCVとグネグネ度",cex.main=2)
points(gam.model$sp,gam.model$gcv.ubre,col=2,pch=18,cex=2)
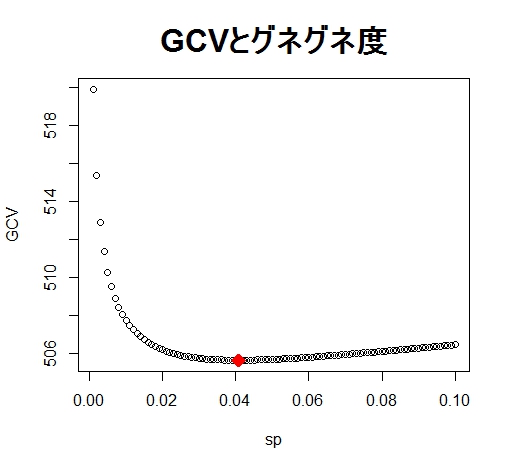
GCVがもっとも小さいグネグネ度を選んでくれていることがわかります。
では、グネグネ度が違うとどんなモデルが出来上がるんでしょうか。グラフを描いて比較してみます。
par(mfrow=c(2,2))
plot(gam(Ozone~s(Temp),sp=1000,data=airquality),residuals=T)
plot(gam(Ozone~s(Temp),sp=1,data=airquality),residuals=T)
plot(gam(Ozone~s(Temp),sp=0.00001,data=airquality),residuals=T)
plot(gam(Ozone~s(Temp,k=20),sp=0.0000001,data=airquality),residuals=T)
par(mfrow=c(1,1))
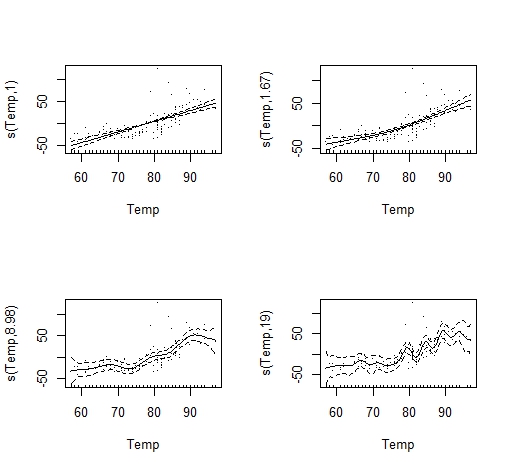
左上→右上→左下→右下 の順番でグネグネ度が大きくなっていっています(spが小さくなるとグネグネします)。それに合わせて引っ張られた線も大
きく異なっていることが見て取れます。
ここで重要なのは、グネグネ度が小さい場合(左上)は、実質、単に直線を引っ張っただけになることです。ようするに、グネグネ度最小の平滑化スプライン
の予測結果と線形回帰の予測結果は一致するということ。
確かめてみましょう。 lm.modoki がグネグネしない平滑化スプラインです。
lm.modoki<-gam(Ozone~s(Temp),sp=100000,data=airquality)
plot(lm.modoki$fitted.values~lm.model$fitted.values,
xlab="線形回帰の予測結果",ylab="グネグネ度最小スプラインの予測結果",cex.lab=1.2)
abline(a=0,b=1,col=2)
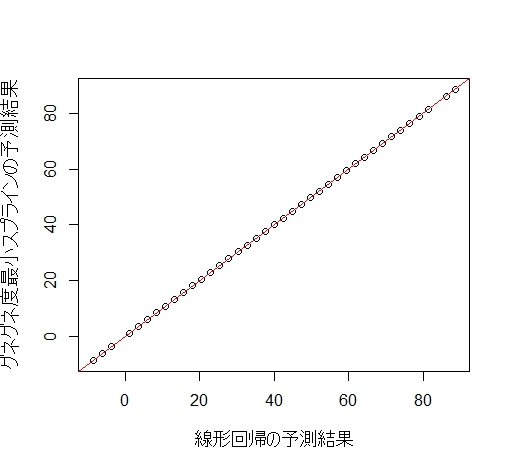
赤い線は切片0、傾き1の直線です。この線上に乗っていることから、両者の予測結果は完全に一致していることがわかります。
以前論文紹介の準備をしていた友人に「加法モデルを使ったって論文には書いてあったんだけど、結果が全然グネグネしてなかったから、先生に『これは加法
モデルじゃないだろう』って怒られた。いったいこれは何の解析をやっているの?」と聞かれたことがあります。加法モデルって書いてある以上は加法モデル
(平滑化スプラインの重回帰バージョン)です。GCVで最適化された推定結果が直線になっちゃったというだけですね。
こんな指摘をされることはあまりないとは思いますが、gam()関数を使うとGCVにより勝手に「線形か非線形か」を判別してくれているというのは覚え
ておいて損はないと思います。とはいえ、GCVの考え方と検定はちょっと違うので、別の方法で確かめておいたほうが無難だとは思いますが。
グネグネ度最小で得られた線形回帰の結果からは傾きの値がいくつなのか知ることは難しいです。なので、線形とみなしてもよい場合はモデル式からs()を
取り除いてやりましょう。加法モデルみたいにたくさんの説明変数があって他の変数にはs()がついていたとしても、一つだけs()を取り除いて計算するこ
とは可能です。
線形回帰のモデルチェック(予測値と実測値の残差が正規分布に従っているか、とか残差の形状がどうなっているかとかを調べる)は
plot(モデル名)
で簡単に表示できました。けれどもgam()を使ったときplot()は計算結果の表示に使われてしまうので、モデルチェックができません。そこで以下の
ようにして表示させます。
gam.check(gam.model)
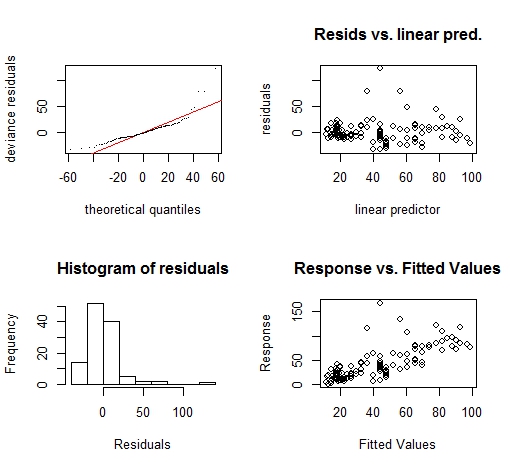
これをみると、左上のQ-Qプロットが直線の上にのっていないし、残差も変な形をしています。
今回扱う内容を超えるので理解できなくても問題ないですが、これは今回予測の対象にしたOzoneが実は正規分布には従っていなかったことが原因です。
Ozoneは0以下の値を取らないため、ガンマ分布などを疑う必要があります(この内容については別のページを設けて説明する予定)。
今回は、あんまりよろしくない結果となってしまったものの、そのまま続けていきます。
さっきは温度とオゾンの関係という一対一の関係を表したモデルでした。
今度は風と温度両方からオゾンを予測してみます。ただし、後で説明する加法モデルとは違って「風が○○でかつ温度が××の時にオゾンが高い」なんていう
組み合わせ(交互作用)を加味した予測を行います。それが薄板平滑化スプラインです。
やり方は簡単。以下のプログラムできれいなグラフが描けます。
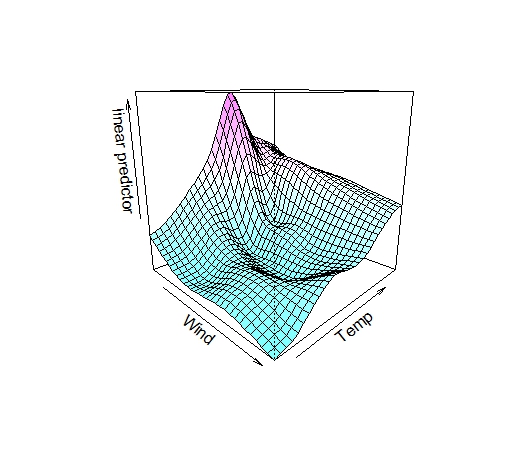
gam2<-gam(Ozone~s(Wind,Temp),data=airquality)
vis.gam(gam2,color="cm",theta=45)
s()の中に二つの変数をいれればモデルはすぐに作れます。結果は今まで通りplot()でも見れますが、より美しいグラフを描くこともできま
す。それがvis.gam()。thetaは横方向への回転です。今回は45度回転させました。縦方向への回転は phi
を指定すればできます。se=Tを指定すれば今までのグラフのように信頼区間を表示してくれます、が、見づらいので省略しました。
等高線を描くこともできます。立体のほうがかっこいいけれど、じつは地味な等高線のほうが可読性高かったりするかも。type="contour"と追加で設定するだけです。
vis.gam(gam2,color="cm",plot.type="contour")
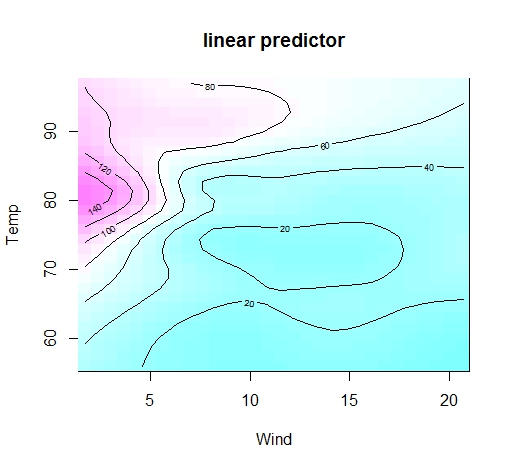
風が弱くてかつ温度が80くらいの時にオゾンが高いことがわかります。
説明変数がたくさんあるときも、こんなグラフを描くことはできます。図は省略しますが、たとえばこんな感じ。
gg<-gam(Ozone~s(Solar.R)+s(Wind,Temp),data=airquality)
vis.gam(gg,view=c("Wind","Temp"),color="cm",theta=45)
興味のある変数を view=c() でくくってやるのがコツ。
ちなみに、 このモデルのように、「薄板平滑化スプライン+普通のスプライン」というモデルのことを(広義の)平滑化スプラインANOVAと呼びます。
いよいよ本番。説明変数を増やした加法モデルを用いて、オゾンを予測してみます。
こちらで示したように説明変数は必要最小限
のものだけを用いる必要があります。今回は重回帰の時のようにAICが最も小さいモデルを採択することにします。
モデルを作る際にGCVとAICと二つも指標を使うのでややこしいんですが、まず変数を入れたときにその変数のグネグネ度を決めるのがGCV。で、そう
やって最適グネグネ度が決められたうえで「その変数って本当に必要か?」を明らかにするのがAICです。
※訂正 2012/6/28
上記の文章を見ると「GCVとは平滑化パラメータを決めるためのもの」であり、AICとは「変
数を選択するためのもの」であるというふうに、明確な使い分けがあるように書かれていますが、これは私の誤りです。実際にはこのように明確な使い分けがな
されるわけではなく、平滑化パラメータをAICで決めることも可能です。今回あつかうモデル選択のやり方では、このような使い分けをしただけであるとご理
解ください。
今回は加法モデルの予測精度と重回帰の予測精度を比較します。
予測精度を比較するとき非常に重要なことがあります。それは
モデルを作るときに使うデータと予測の精度をチェックす
るときに使うデータは別々にする
ということです。
理由は単純。データへの当てはまりは確実に「複雑なモデル」のほうがよくなるからです。たとえばすごくグネグネさせて補間みたいなモデルを作ってやる
と、データ点とのかい離はほとんどなくなり、当てはまりはものすごくよくなります。でも、最初に説明したように、未知のデータを予測することは難しくなっ
てしまいます。
予測の目的は、当然、「まだ起きていないことを予測すること」です。だから未知データを予測するのと同じ状態にするため、テスト用データを別個に用意す
る必要があります。
airqualityデータには欠損値(NA)
がたくさんあります。gam()関数は勝手に欠損値を除いてモデルを推定してくれるんですが、今回は「訓練データ」と「テストデータ」を分けるために欠損
値を取り除きます。
Air<-na.omit(airquality)
length(Air[,1])
> length(Air[,1])
[1] 111
欠損値のないデータセットは111個あることがわかりました。そこで、そのデータセットのうち30個をランダムに選んでテスト用データ (test)とします。学習用データ(teach)はその残りです。
set.seed(1)
S1<-sample(1:111,size=30)
teach<-Air[-S1,]
test<-Air[S1,]
l.model<-lm(Ozone~Solar.R+Wind+Temp,data=teach)
g.model<-gam(Ozone~s(Solar.R)+s(Wind)+s(Temp),data=teach)
変数選択には重回帰の時のようにパッケージMuMInを用います。
library(MuMIn)
a1<-dredge(l.model,rank="AIC")
a1
> a1
Global model call: lm(formula =
Ozone ~ Solar.R + Wind + Temp, data = teach)
---
Model selection table
(Int) Slr.R Tmp Wnd
df logLik AIC delta weight
8 -57.30 0.05952 1.592
-3.693 5 -359.654 729.3 0.00 0.783
7
-56.14 1.721
-3.713 4 -361.939 731.9 2.57 0.217
4 -136.50 0.06107
2.142 4 -369.437 746.9
17.57 0.000
3
-135.80
2.276 3 -371.335 748.7
19.36 0.000
6 80.52
0.09587 -5.745 4 -374.426
756.9 27.55 0.000
5
101.30
-6.060 3 -378.651 763.3 33.99 0.000
2 19.54
0.12300
3 -392.648 791.3 61.99 0.000
1
42.25
2 -397.136 798.3 68.96 0.000
a2<-dredge(g.model,rank="AIC")
a2
> a2
Global model call: gam(formula
= Ozone ~ s(Solar.R) + s(Wind) + s(Temp), data = teach)
---
Model selection table
(Int) s(Slr.R) s(Tmp)
s(Wnd) df logLik AIC delta weight
8 42.25
+
+ + 9
-348.044 713.4 0.00 0.983
7
42.25
+ + 7
-354.079 721.5 8.06 0.017
4 42.25
+
+
7 -362.138 738.6 25.23 0.000
6 42.25
+
+ 6 -364.547 741.8 28.41 0.000
3
42.25
+
4 -367.477 743.5 30.06 0.000
5
42.25
+ 4 -372.917 754.6 41.25 0.000
2 42.25
+
5 -386.463 782.4 69.04 0.000
1
42.25
2 -397.136 798.3 84.87 0.000
重回帰も加法モデルも両方とも変数全部入りモデルが採択されました。というわけで、最初に作ったフルモデルをそのまま使います。
テストデータを予測します。
lm.pred<-predict(l.model,test)
gam.pred<-predict(g.model,test)
予測値と実測値との差の2乗の合計を各々求めます。
lm.resid<-sum((lm.pred-test$Ozone)^2)
gam.resid<-sum((gam.pred-test$Ozone)^2)
lm.resid
> lm.resid
[1] 14211.69
gam.resid
> gam.resid
[1] 8291.634
lm.resid-gam.resid
> lm.resid-gam.resid
[1] 5920.06
加法モデルのほうが予測値と実測値とのずれが小さいことがわかりました。
単純な比較ですが、加法モデルの勝ちです。予測精度は非線形性を加味した加法モデルの方がよいだろうということがわかりました。
比較の方法はこだわればもっといろいろあります(ブートストラップ標本を使うなど)。今回は一例ですが、「とりあえず新しくて複雑なモデルを使う」とい
う考えではなく、きちんと予測精度を見積もって、評価していくという流れが伝われば、と思います。
平滑化スプラインも、加法モデルも、今回示したのより、ほんとはもっともっと複雑です。今回の説明はあくまでも「雰囲気をつかむ」ためのものだと
ご理解ください。
バグや誤り等ございましたら、掲示板などにご一報ください。
参考文献
J.M.チェンバース,T.J.ヘイスティ 編:Sと統計モデル データ科学の新しい波,1994
Simon N. Wood:Generalized Additive Models An Introduction with R, 2006
Julian J. Faraway; Extending the Linear Model with R Generalized Linear, Mixed Effects and Nonparametric Regression Models, 2006
竹澤邦夫:Rによるノンパラメトリック回帰の入門講義
前のページ ⇒ 重回帰 へ
次のページ ⇒ 時
系列解
析 理論編