魚について

Home＞Rによる水産資源解析　＞成長曲線

成長曲線

★新サイト完成しました!
３秒後に自動的に移動します

変わらない方は こちらからどうぞ
http://logics-of-blue.com/%E6%88%90%E9%95%B7%E6%9B%B2%E7%B7%9A/

魚は、大きくなって価値が高くなってから取るのが ベスト。小さいものは獲らず、成長するまで待つことが肝心です。

でも、いったいどれくらい待てばいいの？
　雌雄によって待つ時間は変えたほうがいいの？　一緒でいいの？

この問いに答えるために、魚の成長の特徴を調べ る。これが成長曲線の推定と言う代物です。

サンプルデータとRパッケージ

　今回も、VPAと同じように、とりあえず計算ができればよいという方向で進めて行こうと思います。これは、決して理屈を軽んじて良い というものではなく、管理人の無知により明快な解説ができないという理由からです。詳しい内容は参考文献をどうぞ。
　とはいえ、前回よりかは少し説明部分を増やしました。あまりにも不親切な内容だと思ったので。

　今回はパッケージFSAを用います。

　FSAは「パッケージのインストール」からは落とせません。FSAをインストールするには、以下のコードを実行します。ただし、やや 時間がかかります。

http://www.rforge.net/FSA/Installation.html 　を参考にしてください（英語です）。

source("http://www.rforge.net/FSA/InstallFSA.R")

　library(FSA)
　library(nlstools)

文献1を参考にして、パッケージFSAの中に入っているCroaker2と言うデータを用います。
　どんなデータか見てみます。

data(Croaker2) head(Croaker2) > head(Croaker2)   age  tl sex 1   1 243   F 2   1 247   F 3   1 248   M 4   2 330   F 5   2 320   F 6   2 285   F tapply(Croaker2$tl,Croaker2$sex,summary) > tapply(Croaker2$tl,Croaker2$sex,summary) $F    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.   200.0   326.5   352.0   358.9   410.0   496.0 $M    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.   210.0   292.0   325.0   319.6   343.8   462.0 plot(tl~age,pch=c(21,19)[Croaker2 $sex],col=c(1,2)[Croaker2$sex],data=Croaker2,main="雌雄別年齢体長プロット")　 legend("topleft",legend=c("F","M"),pch=c(21,19),col=c(1,2))

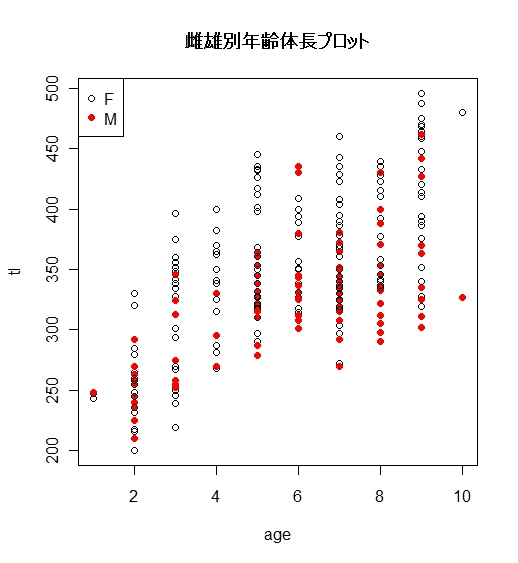
tapplyの結果や、グラフを見ると、雌の方が若干大きそうな感じがします。

　と言うことで、雄雌一緒にしたデータと、雌雄別のデータの両方を用いることとします。雌雄で分けるためのプログラムはこちら。

Croaker.M <- subset(Croaker2,sex=="M") Croaker.F <- subset(Croaker2,sex=="F")

von　Bertalanffy　曲線の推定

上のデータを用いて、代表的な成長曲線の一つである　von　Bertalanffy　曲線を推定してみます。

# 初期値の設定　FSAより vbStarts(tl~age,data=Croaker2,type="typical")    # ワルフォードの定差図から計算されたらしい。 > vbStarts(tl~age,data=Croaker2,type="typical")# ワルフォードの定差図から計算されたらしい。 $Linf [1] 434.697 $K [1] 0.1837369 $t0 [1] -1.635106 # 雌雄まとめたモデル Bertalanffy<-nls(tl~Linf*(1-exp(-K*(age-t0))),data=Croaker2,start=vbStarts(tl~age,data=Croaker2,type="typical")) overview(Bertalanffy) > overview(Bertalanffy) ------ Formula: tl ~ Linf * (1 - exp(-K * (age - t0))) Parameters:       Estimate Std. Error t value Pr(>|t|)    Linf 416.25685   19.34551  21.517  < 2e-16 *** K      0.24180    0.06242   3.874  0.00013 *** t0    -2.17074    0.85673  -2.534  0.01177 *  --- Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 45.33 on 315 degrees of freedom Number of iterations to convergence: 7 Achieved convergence tolerance: 5.816e-06 ------ Residual sum of squares: 647000 ------ Asymptotic confidence interval:             2.5%       97.5% Linf 378.1941042 454.3196044 K      0.1189992   0.3646082 t0    -3.8563856  -0.4851028 ------ Correlation matrix:            Linf          K         t0 Linf  1.0000000 -0.9637789 -0.8779840 K    -0.9637789  1.0000000  0.9674683 t0   -0.8779840  0.9674683  1.0000000 #雌雄別モデル Bertalanffy.M<-nls(tl~Linf*(1-exp(-K*(age-t0))),data=Croaker.M,start=vbStarts(tl~age,data=Croaker2,type="typical")) Bertalanffy.F<-nls(tl~Linf*(1-exp(-K*(age-t0))),data=Croaker.F,start=vbStarts(tl~age,data=Croaker2,type="typical")) #　プロット plot(tl~age,xlab="年齢",ylab= "全長 (mm)",pch=c(21,19)[Croaker2$sex],col=c(1,2)[Croaker2$sex] 　,data=Croaker2,main="雌雄別年齢 体長プロット")  lines(c(1,2,3,4,5,6,7,8,9,10),predict(Bertalanffy, 　　new=data.frame(age=c (1,2,3,4,5,6,7,8,9,10))),lwd=2) lines(c(1,2,3,4,5,6,7,8,9,10),col=2,predict(Bertalanffy.M, 　　new=data.frame(age=c (1,2,3,4,5,6,7,8,9,10))),lwd=2) lines(c(1,2,3,4,5,6,7,8,9,10),col=4,predict(Bertalanffy.F, 　　new=data.frame(age=c (1,2,3,4,5,6,7,8,9,10))),lwd=2) legend("bottomright",legend= c("合わせた","雄","雌"),lwd=2,col=c(1,2,4))

　これもまた、文献1を参考にしました。
　文献3を見ると、重み付き最小二乗法を使った方がよさそうな気がしましたが、文献1を参考にして、今回は重みを設定していません。重み付き最小二乗法を するならば、nls（）の中にweightsを指定してやる必要があります。

　成長曲線は、非線形のモデルに最小二乗法を当てはめて推定するわけですが、毎回初期値をどうしようかと言うことで悩みます。そこで、vbStarts(tl~age,data=Croaker2,type="typical")をします。

　 これは、ワルフォードの定差図を使ってパラメータを推定する関数です。ワルフォードの定差図による推定は統計的な誤りがあるので本来は使ってはなりません が、非線形モデルを推定するための初期値にこれを使ったわけです。FSAの説明書（文献2）にもこの初期値は余り信用しすぎるなと書かれてありますが、こ の値だけを信用すべきと言う確固たる理由は特にないようです。でも、正確な値と割と近そうな初期値を選べるということで、今回も採用しました。

　文献1には、Bertalanffyの成長曲線を推定する別の方法が書かれてありますが、それほど難しいプログラムではないので、自 前で作りました。この方が意味はとらえやすいと思います。

　今回は雌雄を差別しないモデル以外では省略しましたが、overview (モデル)でモデルの詳細を見ることができます。こちらはパッケージnlstoolsの関数で、パラメータの95%信頼区間な ども表示してくれます。

最後のプログラムで、以下のような図が描けます。

雌雄で成長曲線に差があるか、検定

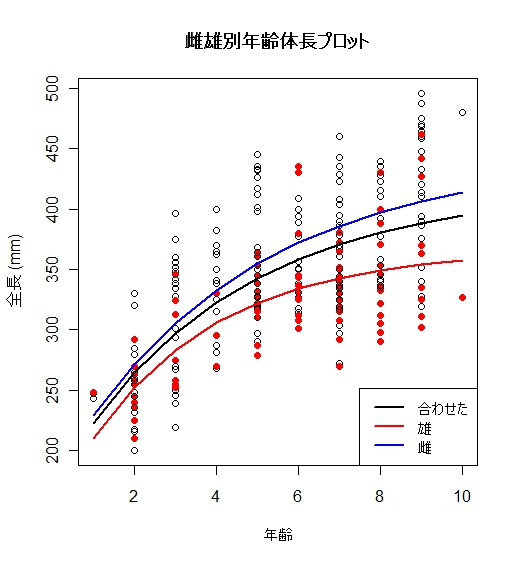
　文献1を参考にしてF検定を実施します。　

　文献1にはR流のモデル選択のやり方が書かれてありますが、ここでは文献3に従って、定義通り計算していこうと思います。

Smf<-deviance(Bertalanffy) Sf<-deviance(Bertalanffy.M) Sm<-deviance(Bertalanffy.F) F<- (Smf-Sm-Sf)/3  / ( (Sm+Sf)/(length(Croaker2$age)-3*2)) F > F [1] 20.24402 1-pf(F,3,length(Croaker2$age)-3*2) > 1-pf(F,3,length(Croaker2$age)-3*2) [1] 5.166978e-12

　RではExcelと異なり、推定されたモデルのパラメータをoverview関数で細かく見れます。また、F検定も比較的楽にできる のではないかと思います。
　尚、重み付き最小二乗法で推定した場合には、F検定で無くχ2検定を行う必要があるようです。

文献1
　FishR Vignette - Von Bertalanfy Growth Models　：Dr. Derek Ogle, Northland College August 25, 2011
　http://www.ncfaculty.net/dogle/fishR/gnrlex/VonBertalanffy/VonBertalanffy.pdf

文献2　FSAの説明書　（PDF)
http://www.rforge.net/src/contrib/Documentation/FSA.pdf

文献3　
赤嶺達郎：水産資源解析の基礎， 恒星社厚生閣, 2007年